结构方程模型SEM

SEM的概念

结构方程模型（Structural Equation Modeling，简称SEM）是基于多元统计分析技术的研究方法，用以处理复杂的多变量数据的探究与分析研究。
    在社会科学以及经济、管理、市场等研究领域，有时需要处理多个原因、多个结果的关系，或者会碰到不可直接观测的变量（即潜变量），这些都是传统的统计方法不易解决的问题。20世纪80年代以来，结构方程分析迅速发展，弥补了传统统计方法的不足，成为多元统计分析的重要工具。

SEM的来源

从发展历史来看，结构方程模式的起源甚早，但其核心概念在1970年代初期才被相关学者专家提出，到了1980年代末期即有快速的发展。基本上，结构方程模式的概念与70年代主要高等统计技术的发展（如因素分析）有着相当密切的关系，随着计算机的普及与功能的不断提升，一些学者（如 Keesing, 1972; Wiley,1973）将因子分析、路径分析等统计概念整合，结合计算机的分析技术，提出了结构方程模型的初步概念，可以说是结构方程模型的先驱者。而后J?reskog与其同事S?rbom进一步发展矩阵模式的分析技术来处理共变结构的分析问题，提出测量模型与结构模型的概念，并纳入其LISREL之中，积极促成了结构方程模式的发展。
    从统计学与方法学的发展脉络来看，结构方程模式并不是一个崭新的技术，而是因子分析（factor analysis）与路径分析（path analysis）两种在社会与行为科学非常重要的统计技术的结合体。相对于这两大分析技术的发展轨迹，Kaplan（2000）指出SEM的历史根源系来自两个重要的计量学科：心理计量学与经济计量学，这两个学术领域对于SEM的发展有着重要的影响。
    心理计量学：
    Spearman认为，人类心智能力测验得分之间的相互关系，可以被视为是由这些分数背后所具有的一个潜的共同因素（common factor）的影响结果。 Thurston认为，在复杂的智力测量背后，应该存在着不同且独立的一组共同因素，他称之为核心心智能力（primary mental abilities），由于这一组共同因素的存在，构成了智力测验得分的复杂关系。研究者必须找出这些因素，才能利用此一因素结构来对智力测验得分之间的共变（协方差）关系，得到最理想的解释，得出最大的解释力。
    经济计量学：
     Haavelmo在1943年利用一系列的联立方程式（simultaneous equation）来探讨经济学变量的相互关系 ，是为经济计量学中的联立方程模型。联立方程模型分析虽然可以用来探讨复杂变量的关系，对于总体经济现象的解释有其效力，但是它所遭到的最大批评在于无法针对特定的经济现象进行精确有效的时间序列性预测。
     SEM应用软件包: LISREL、AMOS、EQS、MPLUS、CALIS、RAMONA等。

SEM的特点:

理论先验性；
    同时处理测量与分析问题；
    以协方差的应用为核心；
    适用大样本分析。

SEM基本模型

简单来说，SEM可分测量方程(measurement equation)和结构方程(structural equation)两部分。测量方程描述潜变量与指标之间的关系，如家庭收入指标等社会经济地位的关系、三科成绩与学业成就的关系。而结构方程则描述潜变量之间的关系，如社会经济地位与学业成就的关系。
    测量模型：对于指标与潜变量(例如六个社会经济指标与社会经济地位)间的关系,通常写成如下测量方程:
    x=Λxξ+δ
    y=Λyη+ε
    x，y是外源(如六项社经指标)及内生(如中、英、数成绩)指标。δ,ε是X，Y测量上的误差。
    Λx是x指标与ξ潜变量的关系(如六项社会经济地位指标与潜社会经济地位的关系)。Λy是y指标与η潜变量的关系(如中、英、数成绩与学业成就间关系)。

Measurement Model测量模型

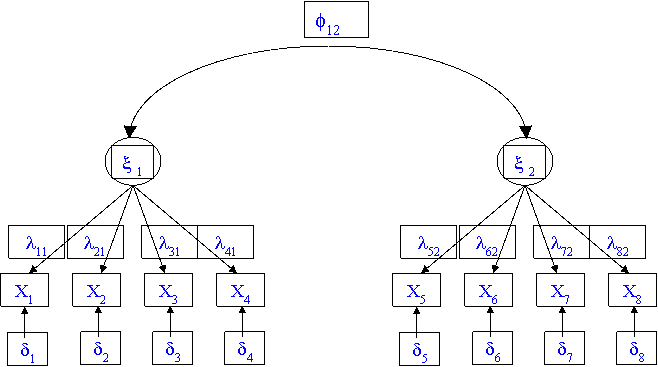
SEM路径图常用图标的含义： 圆或椭圆表示潜变量或因子； 正方形或长方形表示观测变量或指标； 单向肩头表示单向影响或效应； 双向弧形箭头表示相关； 单向箭头指向因子表示内生潜变量未被解释的部分（即残差项）； 单向箭头指向指标表示测量误差。

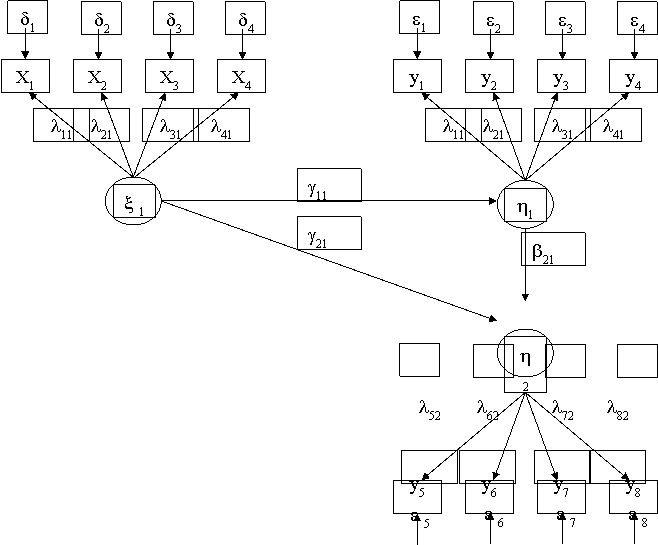
Path Model 结构模型

结构模型：指标(外显变量)含有随机(或系统)性的测量误差，但潜变量则不含这些部份。SEM可用以下结构方程表示潜变量之间的关系（例如社会经济地位与学业成就的关系）：
    η=Bη+Γξ+ζ
    潜变量之间的关系，即结构模型，通常是研究的重点。
    η——内生(依变）潜变量(如学业成就)
    ξ——外源(自变）潜变量(如社会经济地位)
    B——内生潜变量间的关系(如学业成绩与其他内生潜变量的关系)
    г——外源潜变量对内生潜变量的影响(如社会经济地位对学业成就的影响)
    ζ——结构方程的残差项，反映了η在方程中未能被解释的部分。

SEM分析的基本步骤

SEM分析的基本步骤可以分为（概念）模型发展与模型估计修正两个阶段。前者在发展SEM分析的原理基础上并使SEM模型符合特定的技术要求，此时研究者的主要工作在概念推导与SEM分析的技术原理的考虑；后者则是产生SEM的计量数据来评估SEM模型的优劣好坏，并进行适当或必要的修正，此时所着重的是分析工具与统计软件（例如LISREL、EQS、AMOS、MPLUS等）的操作与应用。
    概念模型发展:
    理论性发展：以理论为基础，经过观念的厘清、文献整理与推导、或是研究假设的发展等理论性的辩证与演绎过程，最终提出一套有待检证的假设模型。
    模型设定：发展可供SEM进行检验与估计的变量关系与假设模型。模型设定的具体产品，是建立一个SEM路径图。
    模型识别：只有在模型符合统计分析与软件执行的要求，也就是在能够被有效识别的情况下，SEM分析才能顺利进行。
    模型估计修正:
    抽样与测量；参数估计；拟合检查；模型修正；讨论与结论。

A review of Steps in SEM

Step 1: Developing a theoretically based model (基于理论提出一个或多个基本模型)
    Step 2: Constructing a path diagram of causal relationships
    Step 3: Converting the path diagram into a set of structural equations and specifying the measurement model.
    Step 4: Estimating the proposed model
    Step 5: Evaluating goodness-of-fit (拟合程度) criteria
    Step 6: Interpreting and modifying the model

SEM与回归分析的区别

1、与传统的回归分析不同，结构方程分析能同时处理多个因变量。
    2、同时，回归分析假设自变量为确定、非随机的，即自变量是没有测量误差的，而SEM却没有这样的严格假设。
    3、若各因子可以直接测量（因子本身就是指标），则结构方程模型就是回归分析。

SEM与传统因子分析的不同

1、若不考虑因子间的因果关系，即没有结构模型这部分，则结构方程模型就是传统的探索性因子分析。
    2、与传统的探索性因子分析不同，在结构方程模型中，我们可提出一个特定的因子结构，并检验它是否吻合数据（即验证性因子分析）。

探索性因子分析 VS. 验证性因子分析

相同点:
    相同点：两种因子分析都是以普通因子模型为基础的。因子分析的基本思想是通过变量的相关系数矩阵内部结构的研究，找出能控制所有变量的少数几个随机变量去描述多个变量之间的相关关系，但在这里，这少数几个随机变量是不可观测的，通常称为因子。然后根据相关性的大小把变量分组，使得同组内的变量之间相关性较高，但不同组的变量相关性较低。
    不同点:
    基本思想的差异：探索性因子分析是在一张白纸上作图，而验证性因子分析是在一张有框架的图上完善和修改。是否利用了先验信息？探索性因子分析主要是为了找出影响观测变量的因子个数，以及各个因子和各个观测变量之间的相关程度；而验证性因子分析的主要目的是决定事前定义因子的模型拟合实际数据的能力。验证性因子分析要求事先假设因子结构，我们要做的是检验它是否与观测数据一致。
    分析方法的差异：验证性因子分析是结构方程模型中的一项基本而重要的内容。探索性因子分析——传统因子分析（管理统计中已讲）。主要步骤包括：收集观测变量、获得协方差矩阵（或相关系数矩阵） 、提取因子 、因子旋转 、解释因子结构 、计算因子得分 ；验证性因子分析。主要步骤包括：定义因子模型（选择因子个数和定义因子载荷 ） 、收集观测值 、获得相关系数矩阵、根据数据拟合模型、评价模型是否恰当、与其他模型比较 。

SEM优点

同时处理多个因变量
    容许自变量与因变量含测量误差
    同时估计因子结构和因子关系
    容许更大弹性的测量模型

SEM应用的主要类型

Joreskog & Sorbom（1996）指出SEM的模块化应用策略有三个层次，第一是单纯的验证（confirmatory），也就是针对单一的先验假设模型，评估其适切性，称为验证型研究；第二是模型的产生（model generation），其程序是先设定一个起始模型，在与实际观察数据进行比较之后，进行必要的修正，反复进行估计的程序以得到最佳契合的模型，称为产生型研究；第三是替代模型的竞争比较，以决定何者最能反应真实资料，称为竞争型研究。
    Maccallum & Austin（2000）从文献整理中发现，以单纯的验证与模型产生为目的SEM研究约占20%与25%，涉及竞争比较的SEM研究则有55%。

拟合的概念

当我们测试某一模型时，其实我们在研究自己所提的模型(即哪些变量之间有关，哪些则没有)，是否与数据拟合。
    SEM所输入的是指标变量的样本协方差矩阵(S, sample covariance matrix)，而依我们指定先验(a priori)模式（或称概念模型），计算出一个最佳的衍生矩阵(∑, reproduced/fitted covariance matrix)； S与∑接近，则表示我们建议的模型成立，若S与∑差异大，则表示模型与数据不符。

拟合优度

拟合优度统计量(goodness of fit statistics)反映S与∑间的差异。
    拟合优度指数(CFI)是用于反映E与S差异的一个总指标。当该指数愈接近1，吻合愈好；指数愈小，则表示吻合愈差。
    另外，常用的拟合优度指数还有χ2（越小越好）、NNFI（越接近于1越好）。

简单即最好：一个好的模型是既简单又吻合数据的

我们追求的是既简单又拟合得好的模型。
    “简单”体现在自由度，模型越简单，要估计的参数越少，自由度越多。
    “拟合得好”体现在前面所讲的拟和优度指数。